ในตลาดแลกเปลี่ยนเงินตราต่างประเทศ ผู้ค้าเผชิญกับสองความท้าทายใหญ่
วิธีการจัดการเงินทุนอย่างมีประสิทธิภาพและวิธีการควบคุมความเสี่ยงในการซื้อขาย สูตรเคลลี่ (Kelly Criterion) เป็นกลยุทธ์การจัดการเงินทุนที่มีพื้นฐานทางคณิตศาสตร์ ซึ่งสามารถช่วยผู้ค้าในการเพิ่มผลตอบแทนระยะยาวในขณะเดียวกันก็ลดความเสี่ยง บทความนี้จะวิเคราะห์หลักการของสูตรเคลลี่อย่างละเอียด สำรวจเทคนิคการใช้งานในด้านการจัดการเงินทุนในตลาดแลกเปลี่ยนเงินตราต่างประเทศ และวิเคราะห์วิธีการใช้สูตรเคลลี่ในการจัดการความเสี่ยงในการแลกเปลี่ยนเงินตราต่างประเทศหลักการพื้นฐานของสูตรเคลลี่
สูตรเคลลี่เป็นโมเดลการจัดการเงินทุนที่ใช้ในการคำนวณสัดส่วนการจัดสรรเงินทุนที่ดีที่สุดสำหรับการซื้อขายแต่ละครั้ง เพื่อให้บรรลุการเพิ่มสูงสุดของทุนในระยะยาว สูตรมีดังนี้:สูตร: f* = (bp - q) / b
- f*: สัดส่วนการจัดสรรเงินทุนที่ดีที่สุด (เป็นเปอร์เซ็นต์ของเงินทุนทั้งหมด).
- b: อัตราส่วนกำไรขาดทุน (ผลตอบแทนเฉลี่ยที่ได้จากการขาดทุนแต่ละครั้ง).
- p: อัตราการชนะ (ความน่าจะเป็นของการซื้อขายที่ประสบความสำเร็จ).
- q: อัตราการขาดทุน (ความน่าจะเป็นของการซื้อขายที่ล้มเหลว, q = 1 - p).
เป้าหมายหลักของสูตร: โดยการพิจารณาอัตราส่วนกำไรขาดทุนและอัตราการชนะ สูตรเคลลี่สามารถช่วยผู้ค้าในการบรรลุความสมดุลระหว่างความเสี่ยงและผลตอบแทน เพื่อให้เกิดการเติบโตของเงินทุนอย่างมั่นคงในระยะยาว
ตัวอย่างการใช้งาน: การคำนวณสัดส่วนเงินทุนด้วยสูตรเคลลี่
สมมติว่ากลยุทธ์การซื้อขายของคุณมีดังนี้:- อัตราส่วนกำไรขาดทุนต่อการซื้อขาย (b): 1 ซึ่งหมายถึงการทำกำไรแต่ละครั้งเท่ากับการขาดทุน 1 เท่า.
- อัตราการชนะ (p): 60% ซึ่งหมายถึงความน่าจะเป็นของการซื้อขายที่ประสบความสำเร็จคือ 0.6.
- อัตราการขาดทุน (q): 40% ซึ่งหมายถึงความน่าจะเป็นของการซื้อขายที่ล้มเหลวคือ 0.4 (q = 1 - p).
นำค่าต่างๆ เหล่านี้ไปแทนในสูตร:
f* = [ (1 × 0.6) - 0.4] / 1ผลลัพธ์: ตามสูตรเคลลี่ คุณควรจัดสรรเงินทุน 20% จากเงินทุนทั้งหมดสำหรับการซื้อขายนี้ สัดส่วนนี้สามารถทำให้เกิดการเติบโตของเงินทุนที่ดีที่สุดในระยะยาว
f* = (0.6 - 0.4) / 1
f* = 0.2
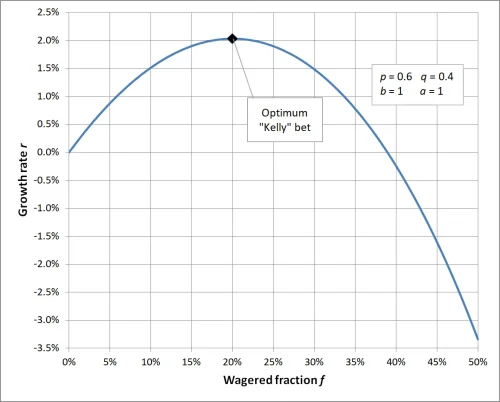
เมื่ออัตราต่อรองในสูตรเคลลี่ตั้งไว้ที่ 1 สัดส่วนการวางเดิมพันที่คำนวณได้คือ 20% ซึ่งหมายความว่าทุกครั้งที่ทำการซื้อขายควรลงทุน 20% ของเงินทุนทั้งหมดเพื่อให้เกิดประสิทธิภาพสูงสุดในการจัดการเงินทุน หากสัดส่วนเงินทุนที่ลงทุนสูงกว่าหรือต่ำกว่าค่านี้ จะทำให้ผลตอบแทนในระยะยาวไม่สามารถบรรลุระดับที่ดีที่สุดได้ สัดส่วนที่สูงเกินไปจะเพิ่มความเสี่ยง ขณะที่สัดส่วนที่ต่ำเกินไปจะไม่ใช้ศักยภาพในการเติบโตของเงินทุนอย่างเต็มที่ สิ่งนี้เน้นย้ำถึงความสำคัญของการจัดการเงินทุนอย่างมีวิทยาศาสตร์ และแสดงให้เห็นถึงบทบาทสำคัญของสูตรเคลลี่ในการควบคุมความเสี่ยงและการเพิ่มผลตอบแทน
การใช้สูตรเคลลี่ในการจัดการเงินทุนในตลาดแลกเปลี่ยนเงินตราต่างประเทศ
1 วิธีการใช้สูตรเคลลี่ในการจัดการความเสี่ยงในการแลกเปลี่ยนเงินตราต่างประเทศ
ตลาดแลกเปลี่ยนเงินตราต่างประเทศมีความผันผวนสูง สูตรเคลลี่สามารถช่วยผู้ค้าในการปรับสัดส่วนการจัดสรรเงินทุนในสถานการณ์ตลาดที่แตกต่างกัน เพื่อควบคุมความเสี่ยงในการซื้อขายอย่างมีประสิทธิภาพตัวอย่าง:
- เมื่ออัตราการชนะและอัตราส่วนกำไรขาดทุนสูง สูตรเคลลี่แนะนำให้ลงทุนเงินทุนมากขึ้นเพื่อแสวงหาผลตอบแทนที่สูงขึ้น.
- ในกรณีที่อัตราการชนะหรืออัตราส่วนกำไรขาดทุนไม่เสถียร ผู้ค้าอาจลดสัดส่วนเงินทุน เช่น ใช้ผลลัพธ์จากการคำนวณสูตรเคลลี่ที่ 50% เป็นการลงทุนจริง.
2 เทคนิคการใช้สูตรเคลลี่
- การเก็บข้อมูลที่แม่นยำ: การคำนวณสูตรเคลลี่ต้องการข้อมูลอัตราการชนะและอัตราส่วนกำไรขาดทุนที่ถูกต้อง ดังนั้นผู้ค้าควรวิเคราะห์บันทึกการซื้อขายเป็นประจำ.
- การปรับสัดส่วนอย่างมีพลศาสตร์: อัปเดตอัตราการชนะและอัตราส่วนกำไรขาดทุนตามการเปลี่ยนแปลงของตลาด เพื่อให้แน่ใจว่าผลลัพธ์ของสูตรเคลลี่ตรงกับสถานการณ์ปัจจุบัน.
- ลดความเสี่ยงที่มากเกินไป: ในทางปฏิบัติ แนะนำให้ลดสัดส่วนเงินทุนที่ได้จากสูตรลงครึ่งหนึ่งเพื่อลดความเสี่ยงที่เกิดจากการใช้เลเวอเรจมากเกินไป.
3 การใช้งานจริงในสถานการณ์การซื้อขายแลกเปลี่ยนเงินตราต่างประเทศ
- กลยุทธ์การซื้อขายตามแนวโน้ม: เหมาะสำหรับตลาดที่มีแนวโน้มที่เสถียร สูตรเคลลี่สามารถช่วยผู้ค้าในการลงทุนเงินทุนมากขึ้นในสถานการณ์ที่มีอัตราการชนะและอัตราส่วนกำไรขาดทุนสูง.
- กลยุทธ์การซื้อขายภายในวัน: สำหรับการซื้อขายที่มีความถี่สูงในระยะสั้น สูตรเคลลี่ต้องใช้ด้วยความระมัดระวัง เนื่องจากความผันผวนของข้อมูลระยะสั้นอาจทำให้ผลลัพธ์การคำนวณเบี่ยงเบน.
บทบาทของสูตรเคลลี่ในการควบคุมความเสี่ยงในการซื้อขาย
ข้อดีของสูตรเคลลี่
- พื้นฐานทางคณิตศาสตร์ของการจัดการเงินทุนในตลาดแลกเปลี่ยนเงินตราต่างประเทศ: สูตรเคลลี่ให้โมเดลทางคณิตศาสตร์ที่ช่วยผู้ค้าในการจัดการเงินทุนอย่างแม่นยำในตลาดแลกเปลี่ยนเงินตราต่างประเทศ.
- ความสมดุลที่ดีที่สุดระหว่างความเสี่ยงและผลตอบแทน: สูตรเคลลี่สามารถเพิ่มผลตอบแทนระยะยาวในขณะเดียวกันก็ควบคุมความเสี่ยงในการซื้อขายแต่ละครั้งอย่างมีประสิทธิภาพ.
ความท้าทายของสูตรเคลลี่
- การพึ่งพาข้อมูล: ความถูกต้องของอัตราการชนะและอัตราส่วนกำไรขาดทุนมีผลโดยตรงต่อประสิทธิภาพของสูตรเคลลี่ ผู้ค้าต้องระมัดระวังในการเก็บรวบรวมและวิเคราะห์ข้อมูล.
- การรบกวนจากอารมณ์: ตลาดแลกเปลี่ยนเงินตราต่างประเทศมีการเปลี่ยนแปลงอย่างรวดเร็ว อารมณ์ของผู้ค้าอาจส่งผลต่อการดำเนินการจัดสรรเงินทุน ทำให้เบี่ยงเบนจากผลลัพธ์การคำนวณ.
วิธีการปรับปรุงการจัดการเงินทุนในตลาดแลกเปลี่ยนเงินตราต่างประเทศด้วยสูตรเคลลี่
- ใช้การซื้อขายจำลองเพื่อทดสอบ: ผู้เริ่มต้นสามารถทดสอบผลกระทบของสูตรเคลลี่ในการซื้อขายจำลอง เพื่อทำความคุ้นเคยกับการจัดการความเสี่ยงในการแลกเปลี่ยนเงินตราต่างประเทศ.
- รวมกลยุทธ์การจัดการความเสี่ยงอื่นๆ: ใช้ร่วมกับการตั้งจุดหยุดการเคลื่อนไหว ,การกระจายสินทรัพย์ ฯลฯ เพื่อลดความเสี่ยงในการซื้อขายเพิ่มเติม.
- ปรับสัดส่วนการลงทุน: ปรับสัดส่วนที่คำนวณได้จากสูตรเคลลี่ตามความผันผวนของตลาด เพื่อหลีกเลี่ยงการขาดทุนที่มากเกินไปจากความไม่แน่นอนของตลาด.
บทสรุป
สูตรเคลลี่เป็นเครื่องมือการจัดการเงินทุนที่ทรงพลัง โดยเฉพาะอย่างยิ่งในการควบคุมความเสี่ยงและการเพิ่มผลตอบแทนในการซื้อขายแลกเปลี่ยนเงินตราต่างประเทศ อย่างไรก็ตาม ความไม่แน่นอนของตลาดต้องการให้ผู้ค้าใช้สูตรเคลลี่อย่างยืดหยุ่น โดยการวิเคราะห์ข้อมูลอย่างแม่นยำและปรับสัดส่วนเงินทุนอย่างมีพลศาสตร์ คุณจะสามารถจัดการความเสี่ยงในการซื้อขายแลกเปลี่ยนเงินตราต่างประเทศได้อย่างมีประสิทธิภาพและบรรลุการเติบโตของทุนอย่างมั่นคงในระยะยาวหากคุณต้องการเรียนรู้เพิ่มเติมเกี่ยวกับการจัดการเงินทุนและการควบคุมความเสี่ยงในการซื้อขายแลกเปลี่ยนเงินตราต่างประเทศ โปรดติดตามเนื้อหาของเราอย่างต่อเนื่อง!
คำถามที่พบบ่อย: เกี่ยวกับสูตรเคลลี่และการจัดการเงินทุนในตลาดแลกเปลี่ยนเงินตราต่างประเทศ
- Q1: สูตรเคลลี่เหมาะสำหรับผู้ค้าแลกเปลี่ยนเงินตราต่างประเทศทุกคนหรือไม่?
A1: สูตรเคลลี่เหมาะสำหรับผู้ค้าส่วนใหญ่ โดยเฉพาะผู้ที่มีกลยุทธ์การซื้อขายที่เสถียรและสามารถสถิติอัตราการชนะและอัตราส่วนกำไรขาดทุนได้อย่างแม่นยำ อย่างไรก็ตาม ผู้ค้าที่ทำการซื้อขายระยะสั้นหรือมีกลยุทธ์ที่มีอัตราการชนะผันผวน อาจไม่เหมาะที่จะพึ่งพาสูตรเคลลี่อย่างเต็มที่เนื่องจากข้อมูลที่ไม่เสถียร. - Q2: หากสัดส่วนการวางเดิมพันที่คำนวณได้จากสูตรเคลลี่เกินขอบเขตความเสี่ยงที่สามารถรับได้จะทำอย่างไร?
A2: เมื่อสัดส่วนที่คำนวณได้จากสูตรเคลลี่สูงเกินไป สามารถเลือกใช้ผลลัพธ์ของสูตรบางส่วน (เช่น 50% หรือ 25%) เป็นสัดส่วนการลงทุนจริง ซึ่งจะช่วยลดความเสี่ยงในขณะเดียวกันก็รักษาความเป็นวิทยาศาสตร์ในการจัดการเงินทุน. - Q3: ทำไมต้องใช้สูตรเคลลี่ในการจัดการความเสี่ยงในการแลกเปลี่ยนเงินตราต่างประเทศ?
A3: สูตรเคลลี่ให้โมเดลทางคณิตศาสตร์ที่ช่วยผู้ค้าในการสร้างสมดุลระหว่างความเสี่ยงและผลตอบแทน และหลีกเลี่ยงการวางเดิมพันมากเกินไปหรือน้อยเกินไป เพื่อให้แน่ใจว่าเงินทุนสามารถเติบโตอย่างต่อเนื่องและมั่นคงในระยะยาวในการซื้อขาย. - Q4: การใช้สูตรเคลลี่ต้องมีเงื่อนไขเบื้องต้นอะไรบ้าง?
A4: การใช้สูตรเคลลี่ต้องการข้อมูลการซื้อขายที่ถูกต้อง ซึ่งรวมถึงอัตราการชนะ (p) และอัตราส่วนกำไรขาดทุน (b) หากข้อมูลเหล่านี้ไม่ถูกต้อง ผลลัพธ์ของสูตรอาจสูญเสียคุณค่าการอ้างอิง. - Q5: หากสภาพตลาดเปลี่ยนแปลงอย่างกะทันหัน ผลลัพธ์การคำนวณของสูตรเคลลี่ยังคงใช้ได้หรือไม่?
A5: เมื่อสภาพตลาดมีการเปลี่ยนแปลงอย่างมีนัยสำคัญ อัตราการชนะและอัตราส่วนกำไรขาดทุนอาจเปลี่ยนแปลงไปด้วย ดังนั้นจึงต้องคำนวณสัดส่วนของสูตรเคลลี่ใหม่เพื่อให้แน่ใจว่าการจัดสรรเงินทุนตรงกับสถานการณ์ตลาดปัจจุบัน. - Q6: สูตรเคลลี่จะใช้ร่วมกับการซื้อขายเลเวอเรจได้อย่างไร?
A6: ในการซื้อขายเลเวอเรจในตลาดแลกเปลี่ยนเงินตราต่างประเทศ สัดส่วนที่คำนวณได้จากสูตรเคลลี่ควรใช้กับเงินทุนจริง (ไม่ใช่เงินทุนหลังจากเลเวอเรจ) และควบคุมจำนวนการสั่งซื้อให้เหมาะสมตามเลเวอเรจ เพื่อหลีกเลี่ยงความเสี่ยงที่มากเกินไป. - Q7: สูตรเคลลี่สามารถรับประกันการทำกำไรในการซื้อขายได้หรือไม่?
A7: สูตรเคลลี่ไม่สามารถรับประกันการทำกำไรได้ เนื่องจากความสุ่มและความไม่แน่นอนของตลาดอาจทำให้เกิดการขาดทุน อย่างไรก็ตาม มันสามารถช่วยผู้ค้าในการเพิ่มอัตราการเติบโตของเงินทุนในระยะยาวภายใต้ความเสี่ยงที่สามารถควบคุมได้. - Q8: ฉันเป็นผู้เริ่มต้น ควรเริ่มต้นใช้สูตรเคลลี่อย่างไร?
A8: ผู้เริ่มต้นควรเริ่มต้นด้วยการสร้างกลยุทธ์การซื้อขายที่เสถียร และบันทึกข้อมูลการซื้อขายในอดีตให้เพียงพอเพื่อคำนวณอัตราการชนะและอัตราส่วนกำไรขาดทุน ทดสอบผลกระทบของสูตรเคลลี่ในเงินทุนขนาดเล็กหรือการซื้อขายจำลอง เพื่อทำความคุ้นเคยกับการใช้งาน.
สวัสดี เราคือ ทีมวิจัย Mr.Forex
การเทรดไม่เพียงแต่ต้องการทัศนคติที่ถูกต้อง แต่ยังต้องการเครื่องมือและข้อมูลเชิงลึกที่มีประโยชน์ เรามุ่งเน้นการรีวิวโบรกเกอร์ระดับโลก การติดตั้งระบบเทรด (MT4 / MT5, EA, VPS) และพื้นฐาน Forex ภาคปฏิบัติ เราจะสอนให้คุณเชี่ยวชาญ "คู่มือการใช้งาน" ของตลาดการเงิน สร้างสภาพแวดล้อมการเทรดแบบมืออาชีพตั้งแต่เริ่มต้นด้วยตัวเอง
หากคุณต้องการก้าวจากทฤษฎีสู่การปฏิบัติ:
1. ช่วยแชร์บทความนี้เพื่อให้เทรดเดอร์มองเห็นความจริงมากขึ้น
2. อ่านบทความเพิ่มเติมเกี่ยวกับ การเรียนรู้ Forex
การเทรดไม่เพียงแต่ต้องการทัศนคติที่ถูกต้อง แต่ยังต้องการเครื่องมือและข้อมูลเชิงลึกที่มีประโยชน์ เรามุ่งเน้นการรีวิวโบรกเกอร์ระดับโลก การติดตั้งระบบเทรด (MT4 / MT5, EA, VPS) และพื้นฐาน Forex ภาคปฏิบัติ เราจะสอนให้คุณเชี่ยวชาญ "คู่มือการใช้งาน" ของตลาดการเงิน สร้างสภาพแวดล้อมการเทรดแบบมืออาชีพตั้งแต่เริ่มต้นด้วยตัวเอง
หากคุณต้องการก้าวจากทฤษฎีสู่การปฏิบัติ:
1. ช่วยแชร์บทความนี้เพื่อให้เทรดเดอร์มองเห็นความจริงมากขึ้น
2. อ่านบทความเพิ่มเติมเกี่ยวกับ การเรียนรู้ Forex